Math 365, Elementary Statistics

Chapter 3 : Probability

Satya Mandal

Introductionback to top

The concept of probability is prevalent at a very basic human intuitive and intellectual level. Other synonyms of probability include likelihood and chances. Probabilistic statements are made on daily basis without any awareness that there may be some intuitive mathematical calculation involved behind such statements.

Most people are aware of different kinds of game of chances and gambling. Examples of such games include tossing coins, any dice rolling game and games of cards. It is universally accepted that when you toss a coin, likelihood of head showing up is fifty percent. When you roll a normal die, it is universally accepted that the likelihood of that a particular face will show up is one in six. There is also awareness of loaded coins and loaded dice, in which likelihood of an outcome (say head or the face six) is higher than that of other outcomes. It is a common sense that in a poker game it is extremely unlikely that one would get three aces in a particular deal. A lot of people would not buy a lottery ticket because they believe that it is extremely unlikely that he or she would ever win a million dollar or would not make money in the long run. These are intuitive or semi-mathematical understanding of probability of occurrence of certain events.

Statements regarding chances of departure of a flights on time would not be so uncommon. Same is true regarding similar statements regarding chances of a thunderstorm, rain, snow or other whether related events. Statements regarding the chances of accidents would be another types probabilistic statements. One would not be surprised to hear a five year old making statements like "I will probably invite Aaron for my birthday". Such would mean that the child is aware of uncertainties of parental permission or his/her own indecisiveness.

When such statement that includes word like "likelihood", "chances" or "probability" are made, one is essentially talking about what they have experienced in the past and trying to project that the same pattern will continue in future.

Some of the early development of Probability as a mathematical theory originated in gambling. In the last century, this concept received further boost in genetics (more generally biosciences) and other branches of science.


3.1 Basic Concept of Probabilityback to top

The concept of Probability attempts to quantify chances (or likelihood) of the occurrence of an event in a consistent manner. It uses human experience of the past to hypothesize and formulate a model. The model needs to behave in a manner that makes an overall sense. For example the chances of occurrence (say of raining today) and nonoccurrence of the same event should add to 100 percent (or probabilities of the same should add to one).

Our experience with tossing normal coins tells us that if we toss a coin for a large number of times, essentially half the time the head shows up. We assume that same pattern will continue in future. Therefore, we hypothesize that the probability that the head will show up is .50. On the other hand, if through extensive experimentation with a coin, we conclude that the ratio of the number of Heads to the number of tosses remains close to and moves around .49 then we would hypothesize that the probability of heads is .49. Such minor difference would be of serious consideration for the gambling houses.

You may like to experiment with the following animation demo of a coin tossing experiment to make your own hypothesis what would be the probability of a particular side:



Similarly, our experience with rolling normal dice tells us that when we roll a die a particular face (say face six) would show up essentially once is six times. So, we hypothesize that probability that face six will show up is 1/6. Contrary to this, there are loaded dice. You may have a loaded die that you experimented with and determined face six shows up 40 percent of the times. So, you would hypothesize that probability that face six will show up for this loaded die is .40.

Similar data may be collected for road accidents and probabilistic hypothesis could be made regarding number of daily accidents on a street.

These examples explain the basic notion of probability. The probability of an event is hypothesized as the "relative frequency", the ratio of occurrences of the EVENT to the total number of times the EXPERIMENT is repeated (or experienced in the past).

Definitions

This section provides basic definitions that will be needed for the rest of the course.

Sets and Subsets

Definition. By a set S we mean a collection of objects. The objects in this set S are also called elements or members of the set. A set E is said to be a subset of a set S if each element of E is also an element of S. We write

E ⊆ S

to mean that E is a subset of S. Obviously, a subset E of S is a smaller collection than or equal to S.

The following are some examples. We also explain the usage of braces to describe a set.

  1. Let D = the collection of all 52 cards in a deck. Then D is a set. Let E be the collection of all the hearts in this deck. Then E is a subset of D. In brace notation

    E={x in D : x is a Heart }

    This is read "E is equal to the set of all x in D such that x is a heart"

  2. Let T be the collection of all those who filed a tax return to the IRS for the year 2001. Then T is a set. Let L be the collection of those whose Adjusted Gross Income in the return was less or equal to $30,000. Then L is a subset of T. Let C be the collection of those who declared capital gains income. Then C is a subset of T. We write
    L ⊆ T
    C ⊆ T
    In brace notation
    L = {x ∈ T : the Adjusted Gross Income of x is less or equal to $30,000}.

    The symbol ∈ means "an element of"
    x ∈ T means x is an element of T

  3. Let N be the collection of all integers, and let E be the collection of even integers. Then N, E are set and
    E ⊆ N
    In brace notation
    N = {n : n is an integer}
    E = {n ∈ N : n is even}.  

  4. Let R be the set of all (real) numbers. Let I be the set of all numbers between 0 and 1, not equal to 0,1. Then R,I are sets and I is a subset of R. In brace notation

    R = {x : x is a real number}
    I = {x ∈ R : 0  <  x  <   1}.   

  5. S = {1,7,13,17,19} is a set.

  6. Let S be the collection of you and your siblings, B be the collection of your brothers, and F be the collection of your sisters. Then S,B,F are sets and we have

    F ⊆ S
     B ⊆ S.

Statistical Experiments and Sample Space

Definitions.

  1. A statistical experiment is a procedure that produces exactly one out of many possible outcomes. All the possible outcomes are known, but which outcome will result when you perform the experiment is not known.
  2. Given an experiment, the set of all possible outcomes is called the sample space. The sample space is usually denoted by S
  3. Given an experiment, an outcome of the experiment is called a sample point. So, the sample space consists of sample points.

Examples. The following are examples of some experiments and their sample spaces.

  1. Suppose the experiment is tossing a coin. The outcomes are H (heads) and T (tails). So, the sample space is S = {H,T}.

  2. Suppose the experiment is tossing a coin twice. The sample points (or outcomes) are HH,HT,TH,TT and the sample space is S = {HH,HT,TH.TT}.

  3. Your experiment is rolling a die. The outcomes are 1,2,3,4,5,6 and the sample space is S = {1,2,3,4,5,6}.

  4. Suppose that the experiment is rolling a die twice. Then the sample space is

S= left bracket (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) right bracket
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

In brace notation, we can write the same as

S = {(i,j) : i = 1,2,3,4,5,6  and j = 1,2,3,4,5,6}.


5. Suppose the experiment is to determine the number of road accidents in Lawrence on a particular day. So, the sample space is S = {0,1,2,3 ... }.


6. Suppose the experiment is to determine the sex of an unborn chlid. Then the sample space is S = {Female, Male}.


7. Suppose the experiment is to determine the blood group of a patient in a lab. Then the sample space is S = {O,A,B,AB}.


8. Suppose the experiment is to observe the annual wheat production in Kansas. Then the sample space is S={x : x is a nonnegative Number} = {x ∈ R : x ≥ 0} =[0, ∞).


9. Suppose that the experiment is rolling a die three times. Then the sam pleican be written as

S = {(i,j, k) : i = 1,2,3,4,5,6  and j = 1,2,3,4,5,6  and k = 1,2,3,4,5,6}.

Definition. The sample space S is called a finite sample space if S has only a finite number of outcomes. If S has infinite elements, it is called an infinite sample space. Note that examples 1, 2, 3, 4, 6, 7 and 9 above have finite sample spaces, and 5 and 8 have infinite sample space.



Events

Definitions. Given an experiment and its sample space S, the following are important definitions.

  1. A subset of the sample space S is called an event. So, an event E consists of outcomes, and we have

    E ⊆ S.

    We say that E would have occurred, if the outcome of the experiment would be in E, when performed.

  2. There is a special event called the empty event or impossible event. It is denoted by ∅. It is defined as the event with no outcomes in it. So, the impossible event consists of no outcome. Therefore, the impossible event would never occur.

  3. Since S is also a subset of itself, S is an event. This event S is called the sure event. Since the outcome of the experiment would always be in S, the sure event S is sure to occur.

  4. A simple event consists of a single outcome.

Remark. Often, we will describe events in "English," and we may have to identify them as a subset of the sample space and also conversely.


Examples. The following are some examples of events.

  1. Look at example 2 above—the experiment on the coin toss. Let E be the event that at least one of the tosses gave T, and let F be the event that both tosses gave the same face. Then

    E = {HT, TH, TT} and F = {HH,TT}.

  2. Look at example 4 above—the experiment on rolling a die. Let E5 be the event that first die showed 5. Then

    E5 = {(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)}.

    Let T5 be the event that the sum of the two "rolls" is 5. Then

    T5 = {(1,4), (2,3), (3,2), (4,1)}.

    Let T1 be the event that the sum of the two rolls is 1. Because T1 has no outcome, it is an impossible event. Let T13 be the event that the sum of the two rolls is 13. Then T13 is also an impossible event.

  3. Look at the example 5 above—the experiment on road accidents. Let E be the event that there is no accident on that day. Then

    E = {0}.

  4. Look at example 8 above—the experiment on annual wheat production. Let E be the event that there will be more than 1000 units of wheat production in 1998. Then

    E = (1000, ∞).

The Definition of Probability

Given a sample space S, in the MATHEMATICS of probability we have hypotheses and rules for how to compute the probability of an event E. Although the MATHEMATICS of probability was modeled based on our past experiences, we do not derive anything from our intuitive ideas. We would be guided by the precise hypotheses, rules and laws that we set up.

For now we will be dealing with finite sample spaces.


Definition. Let

S = { e1, e2, ... ,en }.

be a finite sample space. The probability of a simple event {e} is a number (possibly given) denoted by P({e}) which has the following properties:

  1. 0 ≤ P({e}) ≤ 1.

  2. The sum of the probabilities of all the simple events is 1:

    P({e1}) + P({e2}) + ... + P({en}) = 1.

  3. If E is an event, then the probability P(E), of occurance of E, is defined as the sum of the probabilities of all the sample events in E:

    P(E)= ∑ P({e})
      e ∈ E  
  4. So, we also have

    P(impossible Event)=P (∅)=0

    P(Sure Event)=P(S)=1

3.2 Probability Tables and Equally Likelyback to top


Remark. If we know the probabilities P({e}) of all the simple events {e}, we will be able to compute the probability of any event E using 3. The probabilities of the simple events will

  1. either be given
  2. or a rule or formula will be given to compute it.

Probability with Equally Likely Outcomes

One of the most frequently used models to compute probabilities of simple events is called EQUALLY LIKELY OUTCOMES.

Definition. Let S = {e1, ... , eN} be a finite sample space. We say that all the outcomes are equally likely if all the outcomes have the same probability. So, in this case, we have

P({e1}) = P({e2}) = … = P({eN}) = 1/N.

Also, in this case, for an event E

P(E) = ∑ P({e}) = ∑ 1/N
  e ∈ E   e ∈ E  

=(Number of Outcomes in E)/(Number of Outcomes in S)

If n(E) denotes the number of outcomes in E then

P(E) = n(E)
n(S)
 .

Problems on 3.2

Probability of Simple Events Given in a Table

Exercise 3.2.1. The following table gives the blood group distribution of a certain population.

Blood Group Distribution
Blood Group O A B AB
Percentage of
Population 		47 42 8 3

Find the probability that a random sample of blood will be of Blood Group A or B or AB. (Here S={O, A, B, AB} and we want to compute the probability P(E) of the event E={A, B, AB}.
Solution

Exercise 3.2.2. A student wants to pick a school based on its grade distribution. Following is the most recent grade distribution in a school:

Grade Distribution
Unreal Data
Grades A B C D F
Percentage of
Students 		19 33 31 14 3

Find the probability that a randomly picked student will have at least a B average.
Solution

Exercise 3.2.3. The following table gives the probability distribution of a loaded die.

Probability Distribution for a Die
Face 1 2 3 4 5 6
Probability 0.20 0.15 0.15 0.10 0.05 0.35

Find the probability that the face 2 or 3 or 6 will show up when you roll the die.
Solution

Exercise 3.2.5. An arbitrary spot is selected in a swamp. The depth (in feet) of water in the swamp has the following probability distribution:

Depth Distribution
depth 0+ 1+ 2+ 3+ 4+ 5+ 6+ 7+ 8+
Probability .1 .2 .09 .17 .13 .11 .08 .07 .05
  1. What is the probability that the depth at an arbitrary spot is less than three feet?
  2. What is the probability that the depth at an arbitrary spot is 3 feet or higher?

Solution:
Here, the sample space is S = {0+, 1+, 2+, 3+, 4+, 5+, 6+, 7+, 8+}.

From the table, probability P(0+)=.1, P(1+)= .2, P(2+) = .09 and so on.

  1. Let E be the even that depth at an arbitrary spot is less than three feet.
    Then E = {0+, 1+, 2+}.
    So, P(E) = P(0+)+P(1+) + P(2+)= .1+.2+.09 = .39.
  2. Let F be the event that 3 feet or higher.
    Then F = {3+, 4+, 5+, 6+, 7+, 8+}.
    So, P(F) = P(3+) + P(4+) + P(5+) + P(6+) + P(7+) + P(8+) = .17 + .13 + .11 + .08 + .07 + .05 = .61

Exercise 3.2.6. A Van pool can carry 7 people. Following is the distribution of number of riders in the van on a given day.:

Distribution of number of passengers
number of passengers 1 2 3 4 5 6 7
Probability 0 .12 .22 .23 .28 .08 .07
  1. What is the probability that there will be at most 4 riders?
  2. What is the probability that there will be less than 4 riders?
  3. What is the probability that there will be more than 4 riders?
  4. What is the probability that the van will not be full on a particular day?

Solution:
Here, the sample space is S = {1, 2, 3, 4, 5, 6, 7}.

From the table, probability P(1)=0, p(2)=.12, P(3) = .22 and so on.

  1. Let E be the event that there will be at most 4 riders.
    Then E = {0, 1, 2, 3}. So, P(E) = P(0)+P(1) + P(2) + P(3) + P(4) = 0+ .12 + .22 + .23 = .57.
  2. Let F be the event that 3 there will be less than 4 riders.
    Then F = {0, 1, 2, 3}. So, P(F) = P(0) + P(1) + P(2) + P(3) = 0 + .12 + .22 = .34.
  3. Let G be the event that that there will be more than 4 riders.
    Then, G = {5, 6, 7}.
    So, P(G) = P(5) + P(6) + P(7) = .28+.08+.07 = .43.
  4. Let H be the event that there the van will not be full.
    Then, H = {0, 1, 2, 3, 4, 5, 6}.
    P(H) = P(0) + P(1) + P(2)+ P(3)+ P(4)+ P(5)+ P(6) = 0 + .12 + .22 + .23 + .28 + .08 = .93

Exercise 3.2.7. Following is the distribution of hourly wages (in whole dollars) earned by workers in an industry:

Wage Distribution
Hourly wage in USD 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Probability .04 .06 .07 .09 .11 .12 .14 .11 .09 .08 .04 .03 .01 .01
An employee is selected at random.
  1. What is the probability that the randomly selected worker makes less than 10 dollars an hour?
  2. What is the probability that the randomly selected worker makes at least $10 an hour?
  3. What is the probability that the randomly selected worker makes between $12-$16 an hour?

Solution:
Here, the sample space is S = {7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.

From the table, probability P(7) = .04, p(8)=.06, P(9) = .07 and so on.

  1. Let E be the event that the randomly selected worker makes less than 10 dollars an hour.
    Theb E = {7, 8, 9}. So, P(E) = P(7)+P(8) + P(9) = .04 + .06 + .07 = .17
  2. Let F be the event that the randomly selected worker makes at least $10 an hour.
    Then F = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.
    So, P(F) = P(10) + P(11) +P(12) + P(13) + P(14) + P(15)+ P(16) + P(17) + P18) + P(19) + P(20)
    = .09 + .11 + .12 + .14 + .11 + .09 + .08 + .04 + .03 + .01 + .01 = .82.
  3. Let G be the event that that worker makes between $12-$16 an hour.
    Then, G = {12, 13, 14, 15, 16}.
    So, P(G) =P(12) + P(13) + P(14) + P(15)+ P(16) = .12 + .14 + .11 + .09 + .08 = .54

Exercise 3.2.8. In a school district, the distribution of number of students in a class has the following probability distribution:

distribution of number of students
number of students 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
Probability .03 .04 .06 .07 .10 .12 .13 .11 .09 .07 .06 .04 .03 .02 .02 .01
A child is selected at random from the school district.
  1. What is the probability that the child will be in a class of at least 20?
  2. What is the probability that the child will be in a class of at most 10?
  3. What is the probability that the child will be in a class of less than 10?

Solution:
Here, the sample space is S = {8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23}.

From the table, probability P(8) = .03, p(9)=.04, P(10) = .06 and so on.

  1. Let E be the event that the the child will be in a class of at least 20.
    Theb E = {20, 21, 22, 23}. So, P(E) = P(20)+P(21) + P(22) + P(23) = .03 + .02 + .02 + .01 = .08
  2. Let F be the event that the child will be in a class of at most 10.
    Then F = {8, 9, 10}.
    So, P(F) = P(8) + P(9) + P(10) = .03 + .04 + .06 = .13.
  3. Let G be the event that that child will be in a class of less than 10.
    Then, G = {8, 9}.
    So, P(G) =P(8) + P(9) = .03 + .04 = .07.
Find the Probability with Equally Likely Outcomes

Exercise 3.2.9. An urn contains 7 apples and 3 oranges and 5 pears. One piece of fruit is picked at random. Find the probability that

  1. the fruit is an apple,
  2. the fruit is either an apple or a pear, and
  3. the fruit is an orange.

Solution:
Here, the sample space is S = {A1, A2, A3, A4, A5, A6, A7, O1, O2, O3, P1, P2, P3, P4, P5}.
So, n(S) = 7 + 3 + 5 =15

  1. Let E be the event that the selected fruit is an apple.
    Then E = {A1, A2, A3, A4, A5, A6, A7}.
    So, n(E) = 7
    P(E) = n(E)/n(S)=7/15
  2. Let F be the event that the selected fruit is an apple or a pear.
    Then F = {A1, A2, A3, A4, A5, A6, A7, P1, P2, P3, P4, P5}.
    So, n(F) = 7+ 5 =12
    P(F) = n(F)/n(S)=12/15
  3. Let G be the event that the selected fruit is an orange.
    Then G = {O1, O2, O3}.
    So, n(G) = 3
    P(G) = n(G)/n(S)= 3/15

Solution

Exercise 3.2.10. A die is rolled twice. Find the probability that

  1. the sum is 8,
  2. only 2 or 3 showed up in both the rolls, and
  3. the first roll produced a bigger number.

Solution:
Here, the sample space is

S= left bracket (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) right bracket
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

So, n(S) = 36.

  1. Let E be the event that the sum is 8.
    Then E = {(2,6), (3,5), (4,4), (5,3), (6, 2)} and n(E) = 5.
    So, P(E) = n(E)/n(S) =5/36.
  2. Let F be the event that only 2 or 3 showed up in both the rolls.
    Then, F ={(2,2), (2,3), (3,2), (3,3)} and n(F) =4
    So, P(F) = n(F)/n(S) = 4/36
  3. G be the event that the first roll produced a bigger number. So,
    G= left bracket             right bracket
    (2,1)          
    (3,1) (3,2)        
    (4,1) (4,2) (4,3)      
    (5,1) (5,2) (5,3) (5,4)    
    (6,1) (6,2) (6,3) (6,4) (6,5)  

    So, n(G) = 15.
    P(G) = n(G)/n(S) = 15/36.
  4. Let H be the event that the sum is 1. In fact, sum of the two numbers cannot be 1.
    So, H= impossible event = ∅ and n(H) =0.
    So, P(H) = n(H)/n(S) 0/36=0.

Solution

Exercise 3.2.11. A letter is chosen at random from the letters of the English alphabet. Find the probability that

  1. the letter is either I or U,
  2. the letter is in the word ALWAYS, and
  3. the letter is not in the word NEVER.

Solution:
Here, the sample space is S = {A, B, C, D, E, …, X, Y, Z}.
So, n(S) = 26.

  1. Let E be the event that the selected letter is I or U.
    Then E = {I, U}.
    So, n(E) =2
    P(E) = n(E)/n(S)=2/26.
  2. Let F be the event that letter is in the word ALWAYS.
    Then F = {A, L, W, Y, S}.
    So, n(F) = 5.
    P(F) = n(F)/n(S)=5/26.
  3. Let G be the event that the letter is not in the word NEVER.
    Then G = all letters, except N, E, V, R.
    So, n(G) = 26- 4 = 22.
    P(G) = n(G)/n(S)=22/26.

Solution

3.3 Laws of Probabilityback to top


In the above sections, we defined probability for finite sample spaces. Some of the laws of probability will be discussed in this section. In fact, probability laws are similar to that of law of area, volume or weight.

Notations from Set Theory

Following notations from the set theory will be useful in our context of sample spaces and events.

Notations. Let S be a set and E, F be two subsets of S.

  1. The union E ∪ F, of E and F is the set defined as follows:

    E ∪ F = {x ∈ S : x ∈ E  or x ∈ F}.

    So, if you put together the elements of E and F in a single collection, you get the union E ∪ F.

  2. The intersection E ∩ F, of E and F is defined as follows:

    E ∩ F = {x ∈ S : both x ∈ E and x ∈ F}.


    So, if you take all the elements common to both E and F, you get the intersection of E and F.

  3. The complement Ec, of E is defined as follows:

    Ec = {x ∈ S : x ∉ E}.

    So, the complement Ec of E is the collection of all the elements in S that are not in E.


Remark. It would be adequate, if we can interpret the above definitions in our context of sample spaces and events. For us, S will be a fixed sample space and E,F will be events.

  1. E ∪ F is the event that consists of all outcomes that are either in E or in F (or both). So the occurrence of either E or F is the same as the occurrence of E ∪ F. That is why E ∪ F is also denoted by (E or F).

    E ∪ F = E or F.


  2. E ∩ F is the event that consists of all the outcomes that are both in E and F. So the simultaneous occurrence of E and F is the same as the occurrence of E ∩ F. That is why E ∩ F is also denoted by (E and F). Notationally,

    E ∩ F = E and  F.


  3. Similarly, Ec is the event that consists of all the outcomes in S that are not in E. So, the occurrence of Ec is the same as the nonoccurrence of E. Notationally,

    E c = (not E)

Laws of Probability

Following are some of the laws of probability.

First, probability behaves like area and the laws of probability are like that of area.

Some formulas:
Let S be sample space and let E and F be two events.

  1. We have

    P(E ∪ F) = P( E or F) = P(E)+P(F) - P(E ∩ F)

    = P(E) + P(F) - P(E and F)

    We subtract P(E ∩ F) because we counted it twice: once in P(E) and once in P(F).



  2. Definition. We say E and F are mutually exclusive, if E and F cannot occur simultaneously. This is if E and F have no outcome or E ∩ F = ∅. Since P(∅) = 0, it follows from 1 that

    if E and F are mutually exclusive then

    P(E ∪ F) = P(E) + P(F)

  3. We also have

    P(Ec) = 1 - P(E).

  4. Definition. Let E be an event. We say that the odds of an event E occuring are a to b if

    P(E) = a/(a+b)

Remark: This concept of ODDS is used often in gambling and horse races. When the odds in favor of a horse are 2 to 3, essentially this means that the probability the horse will win is 2/5. We say "essentially" because in actual betting, the probability is actually slightly less than 2/3, so that in the long run the gambling establishment makes more money than it gives. (This instructor is not particularly experienced in such betting or horse races.)

Problems on 3.3: Laws of Probability

Exercise 3.3.1. Let E, F, G be three events. It is given


P(E)=0.3         P(F)=0.7          P(G)=0.6  
P( E ∩ F) = 0.2      P( E ∪ G) = 0.7                      

Find the probability that
  1. E or F occur,
  2. both E and G occur, and
  3. E does not occur.

Solution:

  1. P(E or F)=P(E) + P(F) - P(E and F) = 0.3 + 0.7 - .02 = 0.8
  2. P(E and G) = P(E) + P(G) - p(E or G) = 0.3 + 0.6 - 0.7 = 0.2
  3. P(not E) = 1 - P(E) = 1 - 0.3 = 0.7

Solution

Exercise 3.3.2. Let E, F, G be events .

  1. If the odds in favor of E are 3 to 5, find the probability that E occurs.
  2. If the odds against F are 3 to 4, find P(F).
  3. If P(G) = 7/10, what are the odds in favor of G?


Exercise 3.3.3. The probability that a Christmas tree is taller than 6 feet is .30; the probability that a Christmas tree weighs more than sixty pounds is 0.25; and the probability that a Christmas tree is either taller than 6 feet or more than sixty pounds is .4.

  1. Find the probability that a Christmas tree is both taller than 6 feet and weighs more than sixty pounds.
  2. Find the probability that a Christmas tree is not taller than 6 feet.
  3. Find the probability that a Christmas tree is either less than 6 feet tall or less than sixty pounds in weight.

Solution:
Let E be the event that the selected tree is taller than 6 feet.
Let F be the event that the selected tree is heavier than sixty pounds.
We are given P(E) = 0.30, P(F) = 0.25, and P(E or F) = 0.4

  1. P(E and F) = P(E) + P(F) - p(E or F) = 0.30 + 0.25 - 0.4 = 0.15
  2. P(not E) = 1 - P(E) = 1 - 0.3 = 0.7
  3. In fact not(E and F) is the event thatthe selected tree is either less than 6 feet tall or less than sixty pounds in weight
    P(not(E and F)) = 1 - P(E and F) 1 - 0.15 = 0.85.

Solution

Exercise 3.3.4. The probability that a student majors in liberal arts is .44; the probability that a student majors in business is .33; and the probability that a student majors in either liberal arts or business is .65. Find the probabilities

  1. that a student majors in both liberal arts and business.
  2. that a student majors in neither liberal arts nor business.

Solution:
Let E be the event that the selected student majors in liberal arts .
Let F be the event that the selected student majors in business.
We are given P(E) = 0.44, P(F) = 0.33, and P(E or F) = 0.65

  1. P(E and F) = P(E) + P(F) - P(E or F) = 0.44 + 0.33 - 0.65 = 0.12
  2. In fact, not(E or F) is the event that the selected student majors in neither liberal arts nor business.
    P(not(E or F)) = 1 - P(E or F) = 1 - 0.65 = 0.35

Exercise 3.3.5. In a restaurant menu, entrees are served with rice product or potato product or others. Probability that an entree is served with rice product is .35 , probability that an entree is served with potato product is .40, probability that an entree is served with both is .15. What is the probability that an entree is served with either rice product or potato product?

Solution:
Let E be the event that an entree is served with rice product and F be the event that an entree is served with potato product. We are given
P(E) = .35, P(F) = .40 and P(E and F) = .15.
We need to compute P(E or F).
P(E or F) = P(E) + P(F) - P(E and F) = .35 + .40 - .15 = .60


Exercise 3.3.6. Usual infections can be bacterial or viral. Probability that a person will get a bacterial infection (next winter) is .35, probability that a person will get a viral infection is .65, probability that a person will get either a bacterial or a viral infection is .85.'

  1. What is the probability that a person will get both next winter?
  2. What is the probability that a person will not get an infection next winter?

Solution:
Let E be the event that a person will get a bacterial infection and F be the event a person will get a viral infection. We are given
P(E) = .35, P(F) = .65 and P(E or F) = .85.

  1. We need to compute P(E and F).
    P(E and F) = P(E) + P(F) - P(E or F) = .35 + .65 - .85 = .15
  2. We need to compute P(not (E and F))
    P(not (E and F)) = 1 - P(E or F) = 1 - .85 = .15


Exercise 3.3.7. You go for an examination of upper stomach (EGD) and lower stomach (colonoscopy). Probability that some problem in upper stomach would be found is .15, probability that some problem in lower stomach would be found is .20 and probability that some problem both in lower and upper stomach would be found is .07.

  1. What is the probability that some problem would be found in either upper ot lower stomach?
  2. What is the probability that it would found that both upper and lower stomach are healthy?

Solution:
Let E be the event that some problem would be found in the upper stomach and F be the event that some problem would be found in the lower stomach. We are given
P(E) = .15, P(F) = .20 and P(E and F) = .07.

  1. We need to compute P(E or F).
    P(E or F) = P(E) + P(F) - P(E and F) = .15 + .20 - .07 = .28
  2. We need to compute P(not (E and F))
    P(not (E or F)) = 1 - P(E or F) = 1 - .28 = .72


Exercise 3.3.8. Probability that a person owns a domestic car is .55, probability that a person owns an import is .55 and the probability that a person owns both is .20.

  1. What is the probability that a person owns either a domestic or an import?
  2. Also what is the probability that a person owns none?

Solution:
Let E be the event that a person owns a domestic and F be the event that a person owns an import. We are given
P(E) = .55, P(F) = .55 and P(E and F) = .20.

  1. We need to compute P(E or F).
    P(E or F) = P(E) + P(F) - P(E and F) = .55 + .55 - .20 = .90
  2. We need to compute P(not (E and F))
    P(not (E or F)) = 1 - P(E or F) = 1 - .90 = .10


Problems on the second formula:
Exercise 3.3.9. In a county, 38 percent of the community is a minority. What is the probability that a randomly selected jury will not be a minority?

Solution:
Let E be the event that the jury will be a minority. Then P(E) = .38
Therefore, the answer is P(not E)=1 - P(E)=1 - .38=.62


Exercise 3.3.10. In a school district, probability that a student will be in a class of less than 10 students is .27. The probability that a student will be in a class of less than 20 students is .38. What is the probability that a randomly selected student will be a class 10 or more?

Solution:
Let E be the event that the student will be in a class of less that 10 students. Then, P(E) = .27.
So, the answer is P(not E)=1 - P(E)=1 -.27=.73.


Exercise 3.3.11. In a swamp, probability that the depth at a random spot is higher than 4 feet is .17. What is the probability that at a random spot, the depth is four feet or less?

Solution:
Let E be the event that at a random spot the depth is higher than 4 feet. So, P(E) = .17. So, the answer is
P(not E)=1 - P(E)=1 - .17=.83.


Exercise 3.3.12. It is known that 43 percent of the work force in a town earns more than $37,000 annually. What is the probability that a randomly selected working person would make at most $37,000 annually?

Solution:
Let E be the event that a randomly selected working person would make more than $37,000 annually. Therefore, P(E) = .43.
So, the answer is P(not E)=1 - P(E)= 1 - .43=.57.


Exercise 3.3.13. It is known that you can get an empty seat in the bus 64 percent of the rides. What is the probability that on a particular ride would not get a seat?

Solution:
Let E be the event that you get an empty seat in the bus. So, P(E) = .64. Therefore, the answer is
P(not E)=1 - P(E)=1 - .64=.36

3.4 Counting Techniques and Probabilityback to top

Counting techniques are important and useful. The following are some interesting examples:

  1. the number of English words (formal) of 5 letters, (A formal word is any sequence of letters from the English alphabet. For example, eezq is a formal word.)
  2. the number of ways you can deal a hand of 13 cards from a deck of 52 cards, or
  3. the number of ways you can assign the first row of 11 seats to 231 guests.
Before we go further into counting, let us recall the factorial notation.

Notations. Let n be a positive integer. Then the n! (read as n-factorial) is defined as

n!= 1 . 2 . … (n-2) . (n-1). n

0!=1.

n-factorial is the product of all integers from 1 up to n.


One of the main tools for counting is the following principle:

The Basic Counting Principle. Suppose we have an experiment that is a combination of r sub-experiments, performed one after the other, such that

  1. the first sub-experiment has n1 outcomes;
  2. corresponding to each outcome of the first sub-experiment, the second sub-experiment has n2 outcomes;
  3. corresponding to each outcome of the first and the second sub-experiments, the third sub-experiment has n3 outcomes;


    r. corresponding to each outcome of each of the previous r-1 sub-experiments, the rth sub-experiment has nr outcomes.

Then our original experiment will have n1n2 ... nr outcomes.


Remark. Here we have used the word "experiment" in a slightly different sense than the statistical experiments. The basic counting principle will be used to count the number of outcomes in sample spaces and events.

Animation 3.4.2
Tree Diagrams as an Example
Tree Diagrams and Counting Principle: This demonstrates counting principle, for five tosses.



Examples.

3.4.1. Count the number of words of length five that can be constructed from the English alphabet. Answer: 26x 26x26x26x26

We use the counting principle by dividing this job of constructing a word of length five into five sub-jobs:

Stage Job to do Number of Ways
1. Pick the first letter 26
2. Pick the 2nd letter 26
3. Pick the 3rd letter 26
4. Pick the 4th letter 26
5. Pick the 5th letter 26
  Answer = Product = 11,881,376 words


3.4.2. Count the number of ways you can assign the 11 seats in the first row in a concert hall to 231 guests.
The job of assigning 11 seats can be divided into 11 jobs of assigning each 11 seats.

Stage Job to do Number of Ways
1. Assign seat 1 231
2. Assign seat 2 230
3. Assign seat 3 229
4. Assign seat 4 228
5. Assign seat 5 227
6. Assign seat 6 226
7. Assign seat 7 225
8. Assign seat 8 224
9. Assign seat 9 223
10. Assign seat 10 222
11. Assign seat 11 221
  Answer = Product = 221*222*...*230*231


3.4.3. Contrast: How many ways can you form a committee of 11 members from a group of 231 people? Unlike assigning seats, here the order of selection of the members will be ignored. The 11 members, when permuted around, will have different seat assignments but in the same committee. Forming the committee is a "combination" problem that comes below.


Remark. The difference between assigning 11 seats in a row and forming a committee of 11 is that in the first case the order of assignment is important. Assigning the first row to the same 11 guests in two different ways will count as two different outcomes. When we form a committee, the order in which we pick 11 members does not make any difference.


Definition. Suppose we have n objects. We pick r of them one by one (without ever puttting them back) and arrange them in a row. Such an ordered arrangement will be called a permutation of n objects taken r at a time. The number of permutations of n objects taken r at a time is denoted by nPr. It follows from the basic counting principle that


nPr = n (n-1) (n-2) ... (n-r+1) = n!/(n- r)!

Number of permutations nPr = product of r integers starting from n downward.


Definition. In contrast, we can pick r objects from a collection of n objects one by one but place the object back in the collection before the next pick, and arrange all of them in a row. Such selection and arrangement is called selection with replacment. Constructing a formal word of length 5 is an experiment of picking with replacement.


Definition. Suppose we have n objects in a container. We pick r of them all at a time. In this case the order of selection does not come into consideration. Such a selection is called a combination of n objects taken r at a time. The number of combinations of n objects taken r at a time is denoted by nCr and is given by

nCr =       n!      
(r! (n-r)!)


Examples. 1. Count the number of ways you can form a committee of 11 from a group of 231 people. Answer: 231C11
2. Count the number of ways you can deal a hand of 13 cards from a deck of 52 cards. Answer: 52C13.

Remarks:

  1. Note that n-factorial (n!) grows very fast. In fact, n! is beggar than 2n-1. Like 2n-1, the computers crashes soon if you try to run a program to commute n!.
    If and when you take a course on programming, one of first program you will be asked to write would be the computation of n!.
  2. Likewise, nPr, nCr can also be large.
  3. Following chart illustrates different classification of counting:


Use of Calculators (TI-84):
Computing n-factorial, nPr, nCr
  1. To compute 4! do the following:
    a) type in 4, b) hit the MATH key and scroll to right to PRB, c) scroll down to !, d) ENTER .
  2. To compute 13P4 do the following:
    a) type in 13, b) hit the MATH key and scroll to right to PRB, c) scroll down to nPr, d) type in 4 and ENTER .
  3. To compute 13C4 do the following:
    a) type in 13, b) hit the MATH key and scroll to right to PRB, c) scroll down to nCr, d) type in 4 and ENTER .

Problems on 3.4: Counting Techniques and Probability

Exercise 3.4.1. Find 5!
Solution

Exercise 3.4.2. A homeowner would like to install a new storm door. The local store offers 2 brand names; each brand has 4 different styles and 3 colors. How many choices does the homeowner have?
Solution

Exercise 3.4.3. Suppose in the World Cup soccer tournament, group A has 8 teams. Each team of group A has to play all the other teams in the group. How many games will be played among the group A teams. Answer: 8C2

Exercise 3.4.4. How many ways can you deal a hand of 13 cards from a deck of 52 cards? Answer: 52C13

Exercise 3.4.5. How many ways can you deal a hand of 4 spades, 3 hearts, 3 diamonds, and 3 clubs?
Solution
Solution-variation

Exercise 3.4.6. We have 13 students in a class. How many ways can we assign the 4 seats in the first row? Solution

Exercise 3.4.7. Programming languages sometimes use a hexadecimal system (also called "hex") of numbers. In this system, 16 digits are used and denoted by 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Suppose you form a 6-digit number in a hexadecimal system.

  1. What is the probability that the number will start with a letter digit?
  2. What is the probability that the number is divisible by 16 (i.e., ends with 0)?

Solution
Here the sample space is the collection of all the 5-digit hex numbers.

  • Using the counting principle, the number of hex = n(S) = 166.
  • Let E be the event that the number starts with a letter digit.
  • Again, by the counting principle, the number of hex in E = n(E) = 6*165.
  • So, P(E) = n(E)/n(S) = 6/16.
  • Let F be the event that the number is divisible by 16. Since a number is divisible by 16 means, in hex, the first digit is 0.
  • So, the number of hex in F = n(F) = 165*1 = 165.
  • So, P(F) = 165/166 = 1/16.

Exercise 3.4.8. You are playing Bridge and you are dealt a hand of 13 cards.

  1. What is the probability that you will get a hand of 4 spades, 3 hearts, 3 diamonds and 3 clubs?
  2. What is the probability that you will get all 4 aces?
  3. What is the probability that you will get all 13 spades?

Solution

Exercise 3.4.9. A committee of 9 is selected at random from a group of 11 students, 17 mothers and 13 fathers.

  1. What is the probability that the committee has 3 students, 3 mothers, and 3 fathers, i. e., is a balanced committee?
  2. What is the probability that the committee has 4 mothers and 5 fathers?
  3. What is the probability that the committee has all students?

Solution:
Here total numbter of people in n=11+17+13 = 41. Forming committees are unordered selection.
Total number of committees of 9 members possible = n(S) = 41C9=350,343,565

  1. Let E be the event that the committee consists of 3 students, 3 mothers, and 3 fathers.
    To, count n(E), we make a table for multiplicative principle:
    Stage Job to do Number of Ways
    1. Select 3 studens from 11 11C3=165
    2. Select 3 mothers from 17 17C3=680
    3. Select 3 fathers from 13 13C3=286
      n(E) = Product = 32089200
    So, P(E)= n(E)/n(S) = 32089200/350343565

  2. Let F be the event that the committee consists of 4 mothers and 5 fathers.
    Again, to compute n(F), we make a table:
    Stage Job to do Number of Ways
    1 Select 4 mothers from 17 17C4=2380
    3. Select 5 fathers from 13 13C5=1287
      n(F) = Product = 3063060
    So, P(F)= n(F)/n(S) = 3063060/350343565

  3. Let G be the event that all 9 members of the committee are students.
    Again, this is a combination problem. So
    n(C)=11C9=55
    So, P(G)= n(G)/n(S) = 55/350343565

Solution

Exercise 3.4.10. Three scholarships of unequal value will be awarded from a group of 35 applicants. How many ways can such a selection be made?
Solution

For some additional problems on counting click HERE.

3.5 Conditional Probability and Independent Eventsback to top

Sometimes when new information becomes available, the probability of an event may have to be reevaluated in light of this new information. Suppose we have a sample space S and an event E. Now suppose we have new information that an event C has occurred. We will have to reevaluate the conditional probability of E given that C has occurred. The conditional probability of E given that C has occurred is denoted by P(E|C). Clearly, P(E|C) may be different from P(E). In fact, now that C has occurred, our old sample space is no longer relevant. And C assumes the role of the new sample space.
We give the following definition and formulas.

Definition. Let S be a sample space and E, C be two events.

  1. The conditional probability of E given that C has occurred is
    P(E|C) = P(E∩C)
    P(C)

    if P(C) ≠ 0.

  2. We get the following formula
    P(E∩C) = P(E|C)P(C).

Independent Events

If the conditional probability P(E|F) = P(E) the "simple" probability, then we say that E and F are independent. In this case,

P(E∩F) = P(E)P(F).

Definition. Two events E and F are defined to be independent if

P(E∩F) = P(E)P(F).

If two events are not independent, then they are said to be dependent.

Remark. Let us also describe what we mean by independence of 3 or more events. For events E1,E2, … , En, we say they are independent if the "multiplication rule" applies for any number of them. For example E,F,G,H are independent if all of the following holds:

2 events

P(E∩F) = P(E)P(F),   P(E∩G) = P(E)P(G),

P(E∩H) = P(E)P(H),   P(F∩G) = P(F)P(G),

P(F∩H) = P(F)P(H),   P(G∩H) = P(G)P(H)

3 events

P(E∩F∩G) = P(E)P(F)P(G),   P(E∩F∩H) = P(E)P(F)P(H),  

P(E∩G∩H) = P(E)P(G)P(H),   P(F∩G∩H) = P(F)P(G)P(H)  

4 events

P(E∩F∩G∩H) = P(E)P(F)P(G)P(H)


Example (Justification). Suppose we pick a KU student at random and let E be the event that the student is taller than 6 feet. We have the following:

  1. The sample space S is the whole KU student population.

  2. Since all the outcomes are equally likely, we have
    P(E) = number of KU students who are taller than 6 feet
    Total number of KU students
    		 = n(E)
    n(S)
    		 .

  3. Now suppose we know that the student selected is a male. Let us denote the event that the student is a male by C. The probability that the student is taller than 6 feet, given that the student is a male, is higher than "simple" P(E). In fact, our new sample space is C, which is the whole KU male student population, not S, which is the whole KU student population.

  4. We now have the probability that the student is taller than 6 feet in height given that the student is a male
    = P(E|C) = number of MALE students who are taller than 6 feet
    Total number of male KU- students

    = n(E∩C)
    n(C)
    		 .
    Simple computations show that
    P(E|C) = n(E∩C)/n(S)
    n(C)/n(S)
    		 = P(E∩C)
    P(C)
    		 .

Problems on 3.5: Conditional Probability and Independent Events

Exercise 3.5.1. Let A, B be two events. Given that

P(A) = .66   P(A ∩ B) = .11

Find P(B|A).
Solution

Exercise 3.5.2. Given

P(A|B) = .8 P(B) = .1

Find P(A∩B).
Solution

Exercise 3.5.3. In a certain county, the probability that a person took a flu shot is .45 and the probability that a person will get flu, given that he/she took a flu shot is .06. What is the probability that a randomly selected person took a flu shot and will get flu?
Solution

Exercise 3.5.4. Following are data from a hospital emergency room:

  1. The probability that a patient in the emergency room will have health isurance is 0.75.
  2. The probability that a patient in the emergency room will survive the treatment 0.85.
  3. The probability that a patient in the emergency room will have health insurance and will also survive is 0.7.

What is the conditional probability that a patient in the emergency room will survive, given that he/she has health insurance.

Solution:
Let H = event that that patient has health insurance and S = event that the patient will survive.
Given P(H)=.75,   P(S)=.85,   P(H and S)=.7
P(S|H) = P(S and H)/P(H) = .7/.75 =.9333

Exercise 3.5.5 Following are some statistics about pneumonia:

  1. Probability that an individual will get a pneumonia vaccine shot is .58.
  2. Probability that an individual will get a Pneumonia shot and will get pneumonia in winter is .04.
  3. Probability that an individual will get pneumonia is .13.
What is the conditional probability that a randomly selected person will get pneumonia given that he/she took pneumonia shot?

Solution:
E=event that a randomly selected person ill get a pneumonia vaccine shot,
F=event that a randomly selected person will get a pneumonia
Given P(E)= .58, P(E and F)= .04, P(F)=.13
We have P(F|E) = P(F and E)/P(E)= .04/.58 = .0690

Exercise 3.5.6. Consider the following two circuit diagrams:

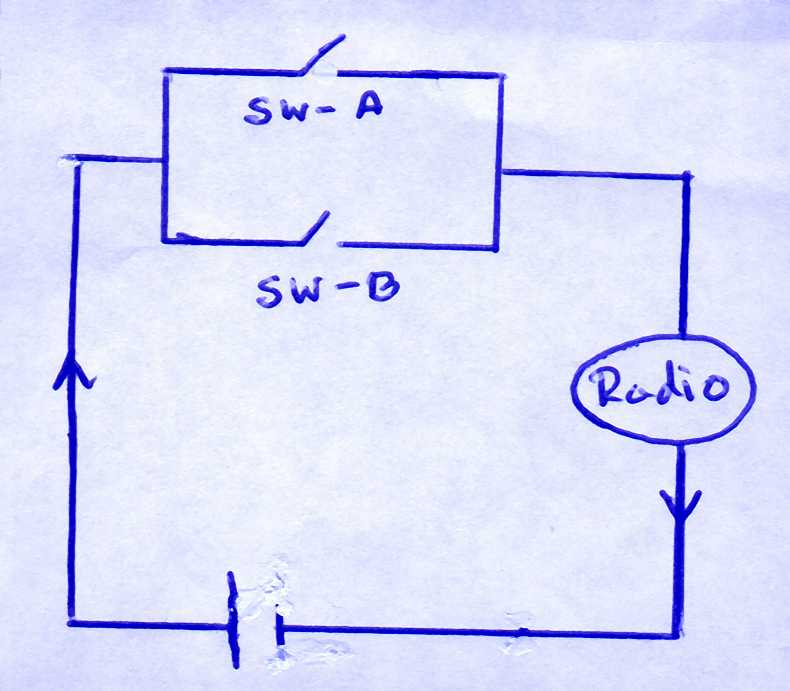
circuit diagram 1
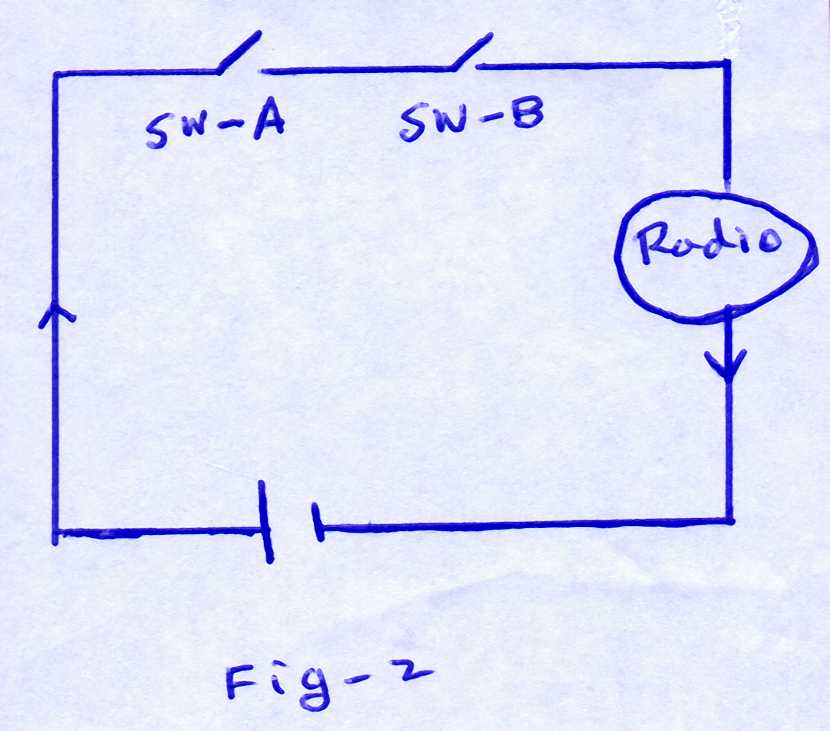
Circuit 1		    circuit diagram 2
Circuit 2


For each of the two circuits do the following:
As you can see, current flows through two switches A and B to the radio and back to the battery. It is given that the probability that the switch A is closed is 0.91 and the probability that the switch B is closed is 0.83. Assume that the two switches function independently. Find the probability that the radio is playing.
Solution

Solution:

    E=the event that Switch A is on (closed) and F= the event that Switch B is on (closed)
    Given P(E)= .91, P(F)=.83
  1. For Circuit 2: In this case:
    P(radio is playing) = P(E and F)=P(E)P(F)= .91*.83= .7553
  2. Circuit 2: In this case,
    P(radio is playing) = P(E or F)=P(E)+P(F) - P(E and F) = P(E)+P(F) -P(E)P(F) = .91+.83 - .91*.83= .9847

Exercise 3.5.7. An airplane has two engines. The probability that engine 1 fails is 0.023 and the probability that engine 2 fails is 0.06. Assume that the engines function independently.

  1. What is the probability that both engines fail?
  2. What is the probability that at most one will fail?
  3. What is the probability that neither will fail?

Solution

Solution:

  1. Let E = event that the engine 1 fails and F = event that the engine 2 fails.
    Then, the event that both fail is (E and F).
    We have P(E)= .023 and P(F) = .06
    Assuming independence,
    P(E and F) = P(E) P(F) = .023*.06 = .00138
  2. P(at most one will fail) = P(not (E and F))= 1-P(Eand F)= 1- .00138= .99862
  3. P(neither fail)= P[(not E) and (not F)]=P(not E)P(not F)= (1-.023)(1-.06)= .91838

Exercise 3.5.8. The probability that you will receive a wrong number call this week is 0.3; the probability that you will receive a sales call this week is 0.8; and that the probability that you will receive a survey call this week is 0.5. What is the probability that you will receive one of each this week? (Assume that all these calls are independent.)
Solution

Solution:
Let E = event that you will receive a wrong number call this week,
F = event that you will receive a sells number call this week,
G = event that you will receive a survey number call this week.
Then, (E and F and G) = the event that you will one of each this week.
We have P(E) = .3, P(F) = 0.8 and P(G) = 0.5.
So, P(E and F and G) = P(E) P(F) P(G) = .3*.8*.5 = .12.

Exercise 3.5.9. Suppose you went for a job interview in Lawrence and another one in Kansas City. Probability of that you will get the job in Lawrence is .25 and the probability of that you will get the job in Kansas City is .33. It is reasonable to assume independence.

  1. What is the probability that you will get both the jobs?
  2. What is the probability that you will get neither?

Solution:
Let E = event that you will get the job in Lawrence and F = event that you will get the job in Kansas City.

  1. Then, the even that you will get both the jobs is (E and F).
    We have P(E)= .25 and P(F) = .33
    Assuming independence,
    P(E and F) = P(E) P(F) = .25*.33 = .0825
  2. The event that you will get neither is ((not E) and (not F)).
    P(not E) = 1-P(E) = 1-.25 = 75, and P(not F) = 1-.33 = .67
    P(Neither) = P((not E) and (not F)) = P(not E)P(not F) = .75 * .67 = .5025

Exercise 3.5.10. You are taking the Elementary Statistics course in KU and your brother is taking the same course in MU. The probability that you will get an A is .18 and the probability that your brother will get an A is .21.

  1. What is the probability that both of you will get an A.
  2. What is the probability that none of you will get an A.

Solution:
Let E be the event that you will get an A and F be the event that your brother will get an A.

  1. Then, the event that both of you will get A is (E and F).
    We have P(E) = .18 and P(F) = .21.
    Assuming independence,
    P(Both) = P(E and F) = P(E)* P(F) = .18 * .21 = .0378.
  2. The event that neither will get A is ((not E) and (not F)).
    P(not E)=1-.18=.82 and P(not F)=1-.21=.79.
    P(Neither) = P((not E)and(not F)) = P((not E)*P(not F)) = .82 * 79 = .6478

Exercise 3.5.11. Probability that you will receive a call from a sibling this week is .35 and the that you will receive a call from a parent this week is .43.(Assume independence.)

  1. What is the probability that you receive a call from both, this week.
  2. What is the probability that you receive a call from neither, this week.

Solution:
Let E be the event that you will receive a call a sibling this week and F be the event that you will receive a call a parent.

  1. Then, the event that you will receive a call from both is (E and F).
    We have P(E) = .35 and P(F) = .43.
    Assuming independence,
    P(Both) = P(E and F) = P(E)*P(F) = .35* .43 = .1505.
  2. The event that neither will call you is ((not E) and (not F)).
    P(not E)=1 - .35 = .65 and P(not F)= 1 - .43 = .57
    P(Neither) = P((not E)and(not F)) = P(not E)*P(not F)) = .65*.57 = .3705

Exercise 3.5.12. Probability that it will rain in Lawrence today is .22 and probability that it will rain today at your home town is .40. (Assume independence.)

  1. What is the probability that it will rain in both places?
  2. What is the probability that it will neither rain in Lawrence nor in your hometown?

Solution:
Let E be the event that it will rain in Lawrence today and F be the event that it will rain at your home town today.

  1. Then, the event that it will rain in both places is (E and F).
    We have P(E) = .22 and P(F) = .40.
    Assuming independence,
    P(Both) = P(E and F) = P(E)*P(F) = .22*.40 = .088.
  2. The event that it will neither rain in Lawrence nor in your hometown is ((not E) and (not F)).
    P(not E)=1 - .22 = .78 and P(not F)= 1 - .40 = .60
    P(Neither) = P((not E)and(not F)) = P(not E)*P(not F)) = .78*.60 = .468

Exercise 3.5.13. According to the poll, probability that a person would vote for Candidate A is .43.

  1. What is the probability that both you and I would vote for Candidate A? (We can assume independence because you and I do not influence each other.)
  2. What is the probability that neither you nor I would vote for Candidate- A?

Solution:
Let E be the event that you will vote for Candidate A and let F be the event that I will vote for Candidate A.

  1. Then, the event that it will rain in both places is (E and F).
    We have P(E) = P(F) = .43.
    Assuming independence,
    P(Both) = P(E and F) = P(E) * P(F) = .43 *.43 = .1849
  2. The event that neither you nor I will vote for Candidate A is ((not E) and (not F)).
    P(not E)=1 - .43 = .57 and P(not F)= 1 - .43 = .57.
    P(Neither) = P((not E)and(not F)) = P(not E)*P(not F)) = .57* .57 =.3249

back to top